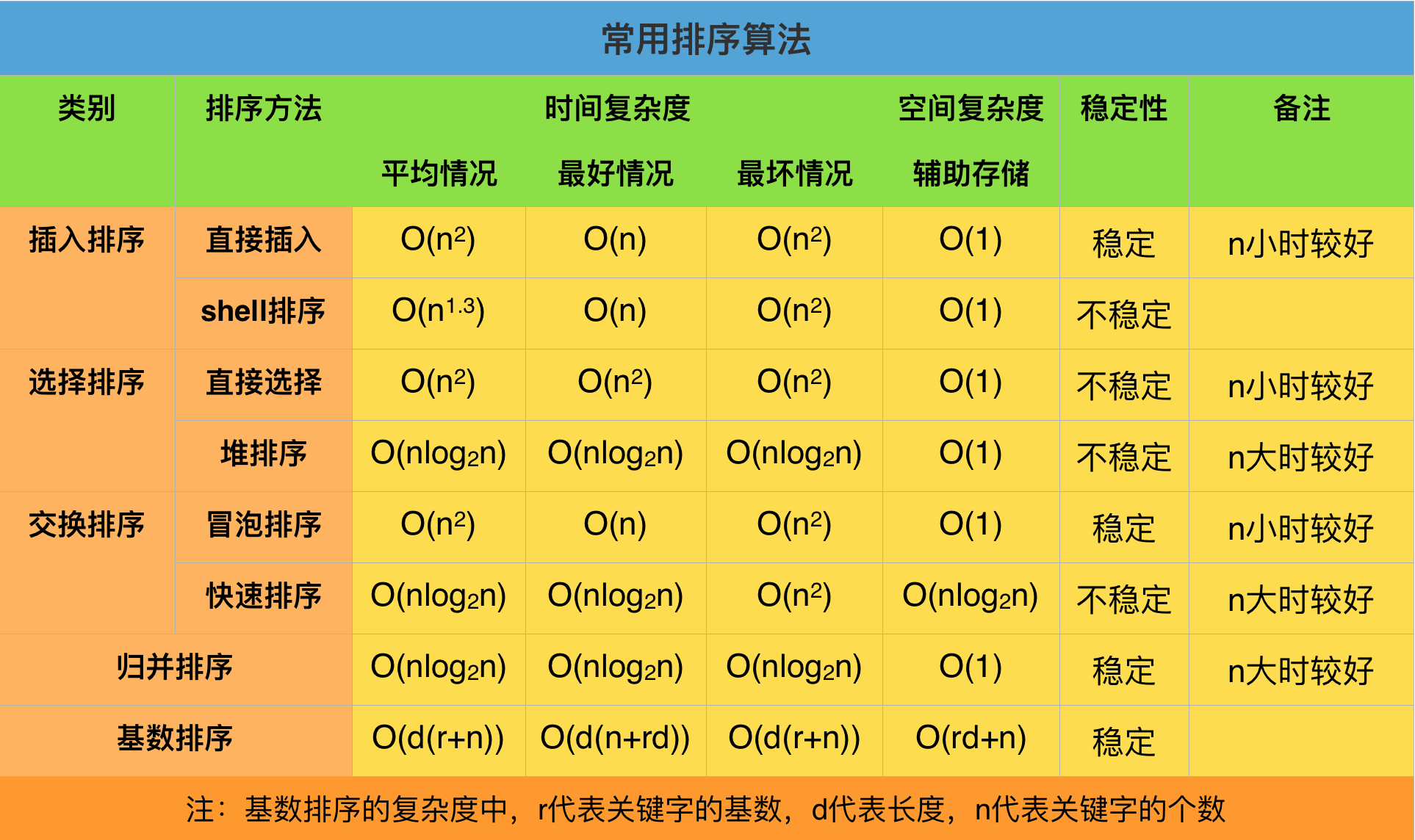
C++排序算法 看了总结图,我这里就总结一下 直接插入排序,冒泡排序,快速排序,堆排序和归并排序,使用C++实现
重新画了总结图
直接插入排序 整个序列分为有序区和无序区,取第一个元素作为初始有序区,然后第二个开始,依次插入到有序区的合适位置,直到排好序
刚开始在我那本《数据结构》看到大概这样的实现
1 2 3 4 5 6 7 8 9 10 void InsertSort(int arr[], int len) { int i, j; int temp; for (i = 1; i < len; i++) { temp = arr[i]; for (j = i - 1; j >= 0 && arr[j] > temp;j--) arr[j + 1] = arr[j]; arr[j + 1] = temp; } }
有点难理解,后来又在网上看到这样的实现,这种方式比较好理解
1 2 3 4 5 6 7 8 9 10 11 void InsertSort(int arr[],int n){ for (int i =1;i <= n;++i){ for(int j = i;j > 0;--j){ if(arr[j] < arr[j -1]){ int temp = arr[j]; arr[j] = arr[j - 1]; arr[j - 1] = temp; } } } }
原理都是一样的,第一个for循环对从第二个开始的所有的数字遍历,嵌套的for循环是每次遍历数字时都取无序区的一个元素与有序区的元素比较,如果比有序区的要小则交换,直到合适的位置。
如果使用vector的话会方便一点,因为vector可以使用size()直接获得容器内的元素个数
1 2 3 4 5 6 7 8 9 10 11 void InsertSort2(vector<int> &num){ for(int i = 1;i < num.size();++i){ for(int j = i;j > 0;--j){ if(num[j] < num[j - 1]){ int temp = num[j]; num[j] = num[j-1]; num[j-1] = temp; } } } }
插入排序的时间复杂度最好的情况是已经是正序的序列,只需比较(n-1)次,时间复杂度为O(n),最坏的情况是倒序的序列,要比较n(n-1)/2次,时间复杂度为O(n^2 ) ,平均的话要比较时间复杂度为O(n^2 )
插入排序是一种稳定的排序方法,排序元素比较少的时候很好,大量元素便会效率低下
这个图很形象,取自维基百科
冒泡排序 比较相邻的元素,如果反序则交换,过程也是分为有序区和无序区,初始时有序区为空,所有元素都在无序区,经过第一趟后就能找出最大的元素,然后重复便可
1 2 3 4 5 6 7 8 9 10 11 12 void BubbleSort(int arr[], int n) { for (int i = 0; i < n - 1; i++) { for (int j = 0; j < n - i - 1; j++) { if (arr[j] > arr[j + 1]) { int temp = arr[j]; arr[j] = arr[j + 1]; arr[j + 1] = temp; } } } }
冒泡排序感觉非常好理解,第一个for循环是遍历所有元素,第二个for循环是每次遍历元素时都对无序区的相邻两个元素进行一次比较,若反序则交换
时间复杂度最坏的情况是反序序列,要比较n(n-1)/2次,时间复杂度为O(n^2 ),最好的情况是正序,只进行(n-1)次比较,不需要移动,时间复杂度为O(n),而平均的时间复杂度为O(n^2 )
但是还有更好的方法,如果第一次比较完没有交换即说明已经有序,不应该进行下一次遍历
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 void BubbleSort(int arr[], int len){ int i,temp; //记录位置,当前所在位置和最后发生交换的地方 int current,last = len - 1; while(last > 0) { for(i = current = 0;i < last;++i){ if(arr[i] > arr[i+1]){ temp = arr[i]; arr[i] = arr[i+1]; arr[i+1] = temp; //记录当前的位置,如果没有发生交换current值即for循环初始化的0 current = i; } } //若current = 0即已经没有可以交换的元素了,即已经有序了 last = current; } }
图取自维基
冒泡排序也是一种稳定的排序算法,也是元素较少时效率比较高
快速排序 快速排序首先选一个轴值(pivot,也有叫基准的),将待排序记录划分成独立的两部分,左侧的元素均小于轴值,右侧的元素均大于或等于轴值,然后对这两部分再重复,直到整个序列有序
过程是和二叉搜索树相似,就是一个递归的过程
排序函数
1 2 3 4 5 6 QuickSort(int arr[], int first, int end){ int pivot = OnceSort(arr,first,end); //已经有轴值了,再对轴值左右进行递归 QuickSort(arr,first,pivot-1); QuickSort(arr,pivot+1,end); }
接下来就是一次排序的函数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 void OnceSort(int arr[], int first, int end){ int i = first,j = end; //当i<j即移动的点还没到中间时循环 while(i < j){ //右边区开始,保证i<j并且arr[i]小于或者等于arr[j]的时候就向左遍历 while(i < j && arr[i] <= arr[j]) --j; //这时候已经跳出循环,说明j>i 或者 arr[i]大于arr[j]了,如果i<j那就是arr[i]大于arr[j],那就交换 if(i < j){ int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } //对另一边执行同样的操作 while(i < j && arr[i] <= arr[j]) ++i; if(i < j){ int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } } //返回已经移动的一边当做下次排序的轴值 return i; }
过程解释都写在注释里面了,挺好理解的
这个图不是一般的棒!!来自维基
快速排序时间复杂度的最好情况和平均情况一样为O(nlog2 n),最坏情况下为O(n^2 ),这个看起来比前面两种排序都要好,但是这是不稳定的算法,并且空间复杂度高一点( O(nlog2 n)
堆排序 堆的结构类似于完全二叉树,每个结点的值都小于或者等于其左右孩子结点的值,或者每个节点的值都大于或等于其左右孩子的值
堆排序过程将待排序的序列构造成一个堆,选出堆中最大的移走,再把剩余的元素调整成堆,找出最大的再移走,重复直至有序
来看一下实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 //堆排序 void HeapSort(int arr[],int len){ int i; //初始化堆,从最后一个父节点开始 for(i = len/2 - 1; i >= 0; --i){ Heapify(arr,i,len); } //从堆中的取出最大的元素再调整堆 for(i = len - 1;i > 0;--i){ int temp = arr[i]; arr[i] = arr[0]; arr[0] = temp; //调整成堆 Heapify(arr,0,i); } }
再看 调整成堆的函数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 void Heapify(int arr[], int first, int end){ int father = first; int son = father * 2 + 1; while(son < end){ if(son + 1 < end && arr[son] < arr[son+1]) ++son; //如果父节点大于子节点则表示调整完毕 if(arr[father] > arr[son]) break; else { //不然就交换父节点和子节点的元素 int temp = arr[father]; arr[father] = arr[son]; arr[son] = temp; //父和子节点变成下一个要比较的位置 father = son; son = 2 * father + 1; } } }
堆排序的时间复杂度最好到最坏都是O(nlogn),较多元素的时候效率比较高
图来自维基
归并排序 归并排序的基本思想是将若干个序列进行两两归并,直至所有待排序记录都在一个有序序列为止
这个图很有概括性,来自维基
我们也可以用递归的思想,每次合并就是一次递归
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 void Merge(int arr[], int reg[], int start, int end) { if (start >= end)return; int len = end - start, mid = (len >> 1) + start; //分成两部分 int start1 = start, end1 = mid; int start2 = mid + 1, end2 = end; //然后递归,分成更小的序列 Merge(arr, reg, start1, end1); Merge(arr, reg, start2, end2); int k = start; //两个序列一一比较,哪的序列的元素小就放进reg序列里面,然后位置+1再与另一个序列原来位置的元素比较 //如此反复,可以把两个有序的序列合并成一个有序的序列 while (start1 <= end1 && start2 <= end2) reg[k++] = arr[start1] < arr[start2] ? arr[start1++] : arr[start2++]; //然后这里是分情况,如果arr2序列的已经全部都放进reg序列了然后跳出了循环 //那就表示arr序列还有更大的元素(一个或多个)没有放进reg序列,所以这一步就是接着放 while (start1 <= end1) reg[k++] = arr[start1++]; //这一步和上面一样 while (start2 <= end2) reg[k++] = arr[start2++]; //把已经有序的reg序列放回arr序列中 for (k = start; k <= end; k++) arr[k] = reg[k]; } void MergeSort(int arr[], const int len) { //创建一个同样长度的序列,用于临时存放 int reg[len]; Merge(arr, reg, 0, len - 1); }
过程解释都写在了注释里
归并排序的时间复杂度都是O(nlogn),并且适用于元素较多的时候排序
参考资料